Grades 4 and 5 NOTES

NOTES...

May 16, 2023

Today we talked about two primary topics:

• How to begin the year to support students with a growth mindset
• How do we model subtraction on a number line?

 Building a Growth Mindset with non-curricular tasks

Here are some collections by grade level of some non-curricular tasks. Use these tasks to establish with students that they are expected to THINK rather than mimic what the teacher teaches. Be sure to review the class norms prior to working on the problem. It is suggested that teachers do 3 to 5 non-curricular tasks to begin the year.

• Grade K/1:  https://docs.google.com/presentation/d/1LCn93LPbLnUsv229LklAtMERSVoSWGoiMt144pkLQRA/edit?usp=sharing 
• Grade 2/3:  https://docs.google.com/presentation/d/1qQdG5BgQdBSZt4izfw8JO3kG5gjqfSNQClbIt80qJ_w/edit?usp=sharing 
• Grade 4/5:  https://docs.google.com/presentation/d/1Z6FIKpaZKu0GRQNj5O_qddHG9TVIvEhgdYY-Y4qTjU8/edit?usp=sharing 
• Grade 6/7/8:  https://docs.google.com/document/d/1EMq1w2gdI--oSN5cRUrItqSzvjQq7VMXwkOu2O1Wz3Q/edit?usp=sharing 

 SUBTRACTION

There are two strategies for thinking about 8 – 3: removal strategy and add-up strategy.

 Removal Strategy and Add-Up Strategy

The Removal strategy is the method many textbooks solely focus upon. To model 8-3, you would start at 8 on the number line and then go backwards (remove) 3. Since we end up on 5, the answer to 8-3 is 5.

This method is particularly effective when the number being removed is fairly small.

87 - 4

13 - 2

1249 - 7

…these problems are particular well-suited for using the Removal Strategy.

Add-Up Strategy

A second strategy for solving a subtraction problem is the Add-Up Strategy. In this strategy you think of the subtraction problem as an addition problem with a missing addend. Therefore, to solve 8-3, you would think "3 plus what equals 8?". 

3 + ⃞ = 8

Said in another way, "how many hops do I need to make to go from 3 to 8?"

This method is particularly effective when the number being removed (minuend???) is fairly close to the first number (subtrahend????).

87 - 82

13 - 9

1249 - 1500

…these problems are particularly well-suited for using the Add-Up Strategy.

Examples of Add-Up strategy on a number line

It is important to allow students to share their MANY different ways to arrive at the answer using the same model and strategy.

Here are three different ways to use the Add-Up strategy for 1235 – 897:

The Add-Up strategy also works for fractions!!!

 

 

 

 

February 7, 2023

 We talked about CRA today.

Using dots to model long division.

  

Using tape diagrams to model fraction addition

  

Using tape diagrams and number lines to represent subtraction.

 

 

 

October 25, 2022

Today we focused mostly on expanding our understanding of the strategies and models we want our 4th and 5th grade students to know.

Here is the list of essential strategies: http://bit.ly/Strategies-and-Models

What visual representation might we use for 2-digit by 2-digit multiplication problems? We can use dots or area model.

Here are the dots... (The area model is in the lower left corner of the photo.)

 

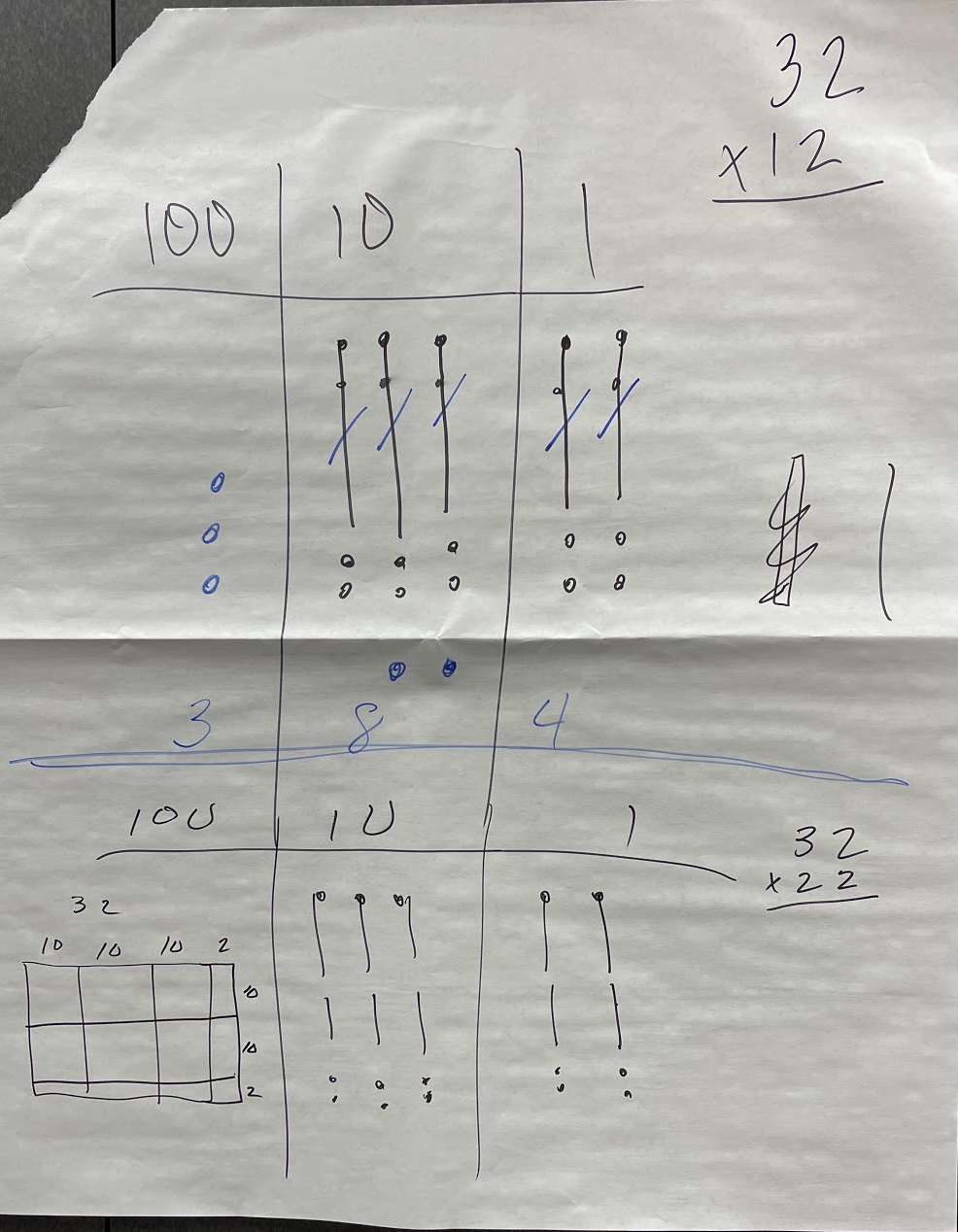
A couple of ways to model division. Area model and dots.

We want to use dots because dots will extend into decimals, while the area model does not allow us to extend into decimals.

 

Here is a playlist of several videos I made showing a variety of ways to do long division:
https://youtube.com/playlist?list=PLvolZqLMhJmkMPmBH-oel9ufT_7dwk_v4

 We then wrapped up our time by studying each of the four essential multiplication strategies and how to model them.

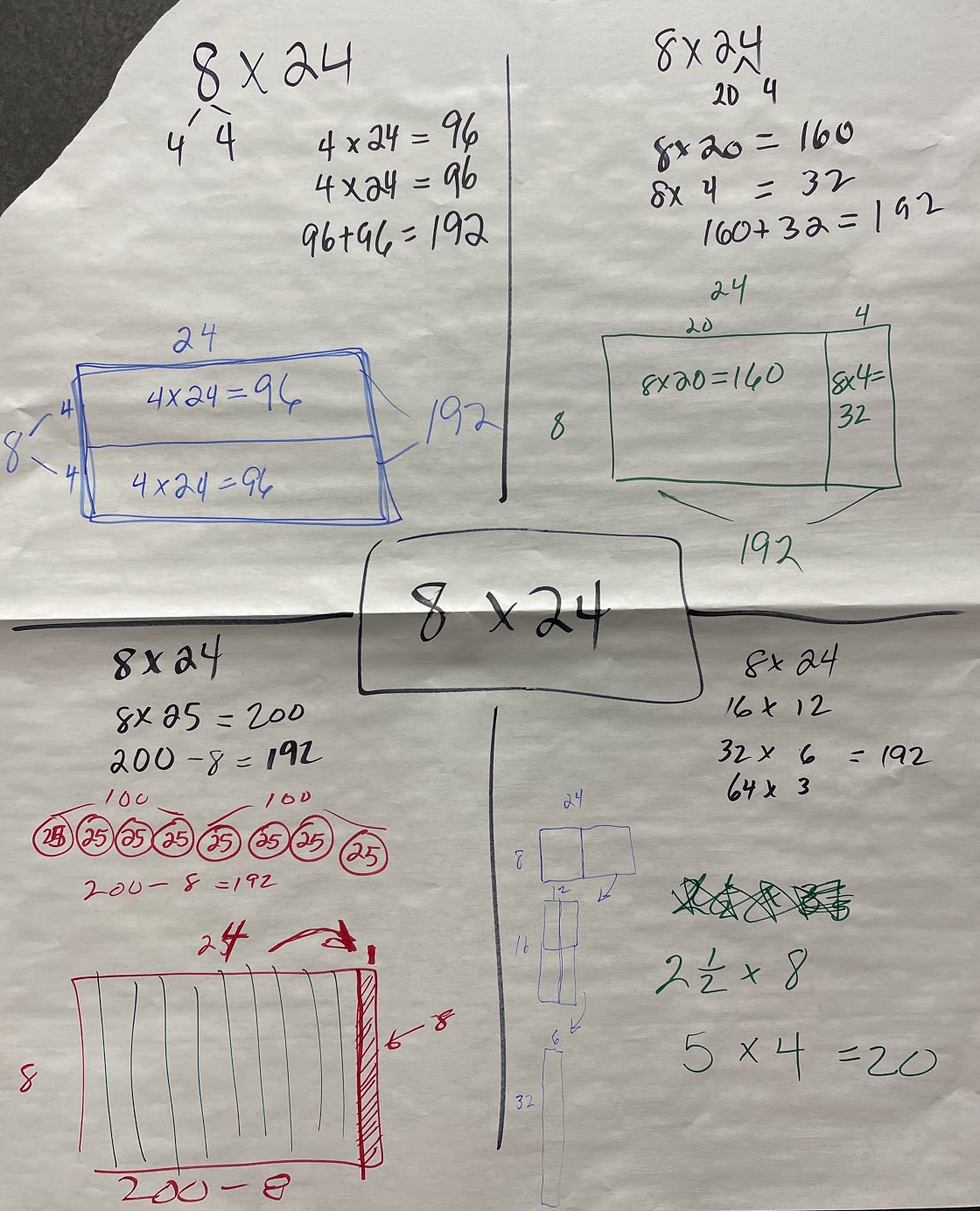
NEXT STEPS:

• How can we apply the principles of CRA to our daily curriculum?
• How might we incorporate Desmos/Polypad into our instruction?